עיין בדוגמת הרשת הבאה:
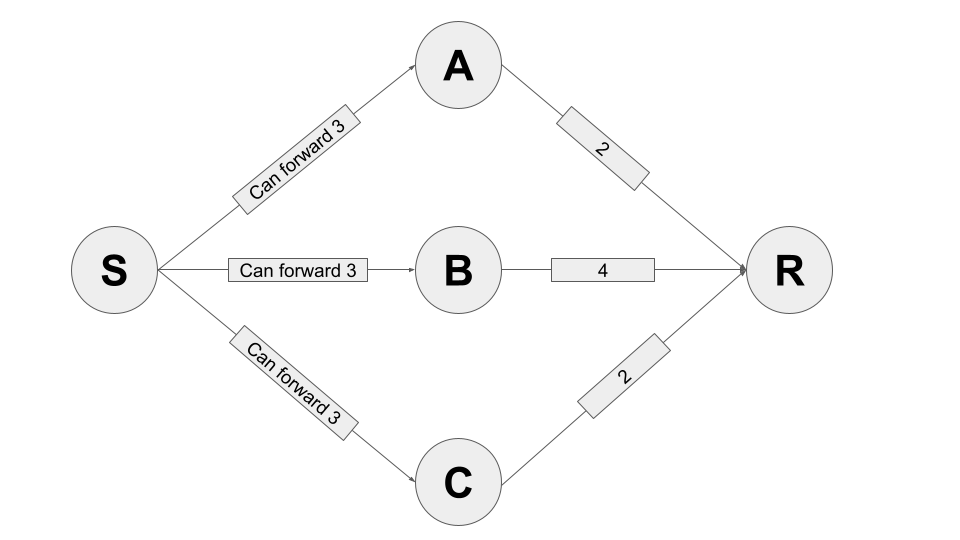
לְהַנִיחַ S רוצה לשלוח 3 SATS אל Rו אתה יכול להניח עוד S יש מספיק נזילות בכל אחד מהערוצים המקומיים שלה כדי לשלוח אליו 3 SATS. נניח גם את הנזילות בערוצים (A,R), (B,R) וכן (C,R) מופץ באופן אחיד.
זרימת תשלום אמינה אחת בתרשים זה נראית כך:
1 sat: S --> A --> R probability: 2/3
2 sats: S --> B --> R probability: 3/5
לזרימה זו יש הסתברות מוחלטת 2/3*3/5 = 2/5 = 0.4 = 40%
השאלה:
כיצד לחשב את הערך הצפוי של סאטושיס להגיע אליו R אִם S שולח 3?
אפשרות א
(שאני כבר יודע שזה לא בסדר אבל אני כותב את זה כי אני חושד שיש אנשים שיש להם מחשבה ראשונה דומה)
בתחילה חשבתי שזה פשוט יהיה 3 sats * 2/5 = 6/5 sats = 1.2 sats וזה מה שמקבל מכפלת הכמות לשלוח עם ההסתברות לזרימה. זה נראה מוזר כששלח 2 SAT יחד S-->B-->R יש הסתברות ל 3/5 ועם הנמקה של לעיל ערך ציפייה של 2 sats * 3/5 = 6/5 sats = 1.2 satsו מכיוון שהערך הצפוי עבור 1 ישב לאורך S-->A-->B הנתיב גדול מ 0 זו תהיה סתירה לתוספות של הערך הצפוי.
אפשרות ב
החל מההנמקה לעיל אנו מוסיפים את הערכים הצפויים לנתיבי המפרקים כך:
E(3 sats) = 1 sat * 2/3 + 2 sat * 3/5 = 10/15 sats + 18/15 sats = 28/15 sats
אפשרות ג
כמובן שני שביל סאטושי S-->B-->R לא צריך לשלוח כבצל אחד אך ניתן לשלוח אותו כשני בצל עם 1 ישב כל אחד:
לראשון יש הסתברות 4/5 ולשנייה יש הסתברות מותנית ל 3/4 שמוסבר בהרחבה בנושא זה. עם ההיגיון מאפשרות B צריך להיות מסוגל להוסיף ערכים צפויים אלה. אז יש לנו את הערך הצפוי לשליחת שני SAT בשני בצל שבת נפרד 1 S--> B --> R יחושב כ:
E(2 sats) = 1 sat * 4/5 + 1 sat * 3/4 = 31/20 sats
אם נוסיף את בצל השבת 1 מה- S-->A-->R שהיה 2/3 SATS
היינו מצפים שיהיה לנו
E(3 sats) = 31/20 sats + 2/3 sats = 93/60 sats + 40/60 sats = 132/60 sats = 33/15 sats
זֶהוּ 5/15 sats = 1/3 sats יותר מהתשובה באפשרות B
אפשרות ד
כדי להחמיר את המצב אני מבולבל אם הערכים הצפויים של ניתוק 2 הבצל השבת באופציה C לשני בצל SAT 1 יכולים פשוט להוסיף באופן ליניארי מכיוון שהבצל השני מותנה על כך שיש 2 SATs של נזילות בתעלה. אם הבצל הראשון נכשל, השני בוודאי ייכשל. כך היה צריך לחשב את הערך הצפוי לשליחת שני בצל ישב כזה:
E(2 sats) = 1 sat * 4/5 + 1 sat * 3/5 = 7/5 sats
זה יביא לערך הצפוי הכולל של:
E(3 sats) = 2/3 sats + 7/5 sats = 10/30 sats + 21/15 sats = 31/15 sats
מחשבות
רק לשם השוואה הנה התוצאות
- אפשרות א:
18/15 - אפשרות ב:
28/15 - אפשרות ג:
33/15 - אפשרות ד:
31/15
בעוד שאפשרות B נראית בהחלט צודקת, הגיוני לנתח עוד יותר את שני בצל SATS. בהדמיות עשיתי נראה כי אפשרות D נכונה וזה קצת מפתיע עבורי. השימוש בפורמליזם של תיאוריית ההסתברות ההבדל עבור 2 מסלול ה- SAT הוא:
- אפשרות ג:
E(2 sats) = 1 sat * P(X>=1) + 1 sat * P(X>=2 | X >= 1) - אפשרות ד:
E(2 sats) = 1 sat * P(X>=1) + 1 sat * P(X>=2)
כאמור, ההגדרה המדומה מצביעה על כך שאפשרות D היא התשובה הנכונה, אך זה מפתיע לי מאוד מכיוון שהייתי מצפה שהמונח השני יהיה הסתברות מותנית.


